Flow curve with yield point

The lowest needed shear stress
for getting the sample to flow.
for getting the sample to flow.
Pasty and creamy samples, sealants, but also solids like steal exhibit a so called Yield point. These samples don't flow until the applied shear stress exceeds a certain value, namely the yield stress.
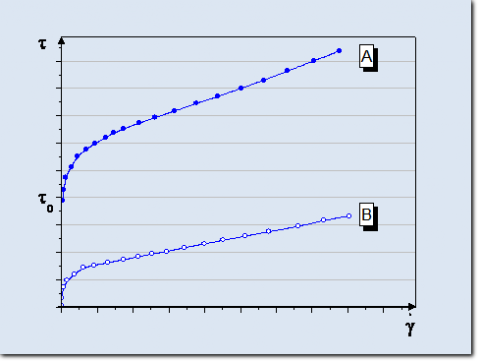
Flow curve of samples with (A) or without (B) yield point.
The yield point is usually determined by extrapolating a flow curve to zero shear rate. Therefore the experimental data of the flow curve has to be fitted with a regression model, e.g. Bingham, Casson or Herschel-Bulkley. The different models normally don't lead to the same yield point value. Thus always the same model should be used in order to be able to compare results from different samples.
Often it is better to determine the yield point by analyzing the experimental data at low shear stresses below t0.
Below the yield strength the samples exhibit elastic deformation behaviour and often a creeping with high viscosities. For the analysis it is recommended to plot the logarithm of the deformation against the logarithm of the shear stress.
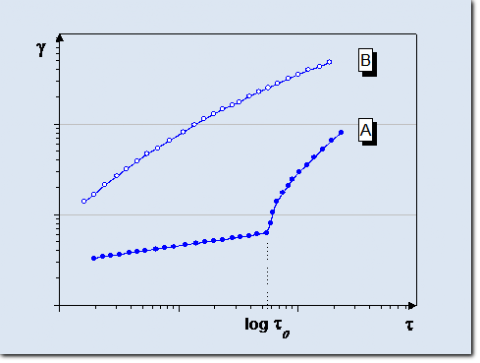
Determination of the yield point by means of analysis of the elastic deformation below the yield point.
In the ideal case of a linear-elastic deformation without creeping in a log- / log- plot the slope below the yiel point is unity. As soon as the shear stress exceeds the yield point the deformation increases more than proportional with the stress: The flow curve exhibits an abrupt change in the slope.
Strictly speaking, a lot of samples that exhibit a yield poin also flow below t0. The reason is the creeping which often appears below the yield point. Samples that show a smooth transition from elastic deformation via creeping to real flow do not show a sharp increase in the slope of the log-g / log-t plot. In these cases the yield point is better determined by means of an amplitude sweep.
